


A、1
B、2
C、3
D、 不可能有这样的树
答案:B
解析:解析:设度为3的结点数为x,度为1的结点数为y,则树的总结点数为度为3的结点数+度为2的结点数+度为1的结点数+度为0的结点数,即为x+0+y+5。再根据树的总结点数为树中所有结点的度数之和再加1,则总结点数为3×x+2×0+1×y+O×5+1。 x+y+5=3×x+y+1,则x=2,所以度为3的结点个数为2。本题答案为B选项。



A、1
B、2
C、3
D、 不可能有这样的树
答案:B
解析:解析:设度为3的结点数为x,度为1的结点数为y,则树的总结点数为度为3的结点数+度为2的结点数+度为1的结点数+度为0的结点数,即为x+0+y+5。再根据树的总结点数为树中所有结点的度数之和再加1,则总结点数为3×x+2×0+1×y+O×5+1。 x+y+5=3×x+y+1,则x=2,所以度为3的结点个数为2。本题答案为B选项。



A. ABCDEFGH
B. ABCDHGFE
C. DCBAHGFE
D. HGFEDCBA
解析:解析:二叉树遍历可以分为3种:前序遍历(访问根结点在访问左子树和访问右子树之前〉、中序遍历(访问桐结点在访问左子树和访问右子树两者之间)、后序遍历(访问根结点在访问左子树和访问右子树之后),并且在遍历左右子树时也遵循同样的规则。本题中,二叉树的前序序列与中序序列的为.ABCDEGH,可确定该二叉树的报接结点为A且结点A没有左子树,后序序列最后访问的是根结点A,只有D项满足。本题答案为D选项。
A. ABDHECFG
B. ABCDEFGH
C. HDBEAFCG
D. HDEBFGCA
解析:解析:
完全二叉树是指除最后一层外,每一层上的节点数均达到最大值,在最后一层上只缺少右边的若干节点。完全二叉树按层次输出的序列为ABCDEFGH,则二叉树如下图所示。该二叉树的中序序列为HDBEAFCG。本题答案为C选项。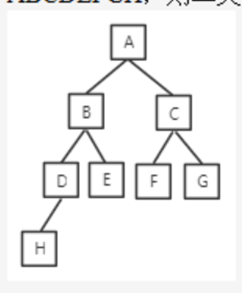
A. HFDBGECA
B. ABCDEFGH
C. HGFEDCBA
D. ACEGBDFH
解析:解析:二叉树遍历可以分为3种:前序遍历(访问根结点在访问左子树和访问右子树之前)、中序遍历(访问桐结点在访问左子树和访问右子树两者之间)、后序遍历(访问相结点在访问左子树和访问右子树之后),并且在遍历左右子树时也遵循同样的规则。本题中,二叉树的前序序列为.ABDFHCEG,,可确定该二叉树的相结点为A,后序序列最后访问的肯定是相结点A,排除B、D两项。再根据中序序列为HFDBACEG,可确定结点A的左子树的相结点是B,右子树的相结点是C,则后序序列倒数第2个访问的肯定是结点c,排除C选项。本题答案为A选项。
A. ABCDEF
B. CBAFED
C. FEDCBA
D. DEFCBA
解析:解析:二叉树煽历可以分为3种:前序遍历(访问根结点在访问左子树和访问右子树之前〉、中序遍历(访问相结点在访问左子树和访问右子树两者之间)、后序遍历(访问根结点在访问左子树和访问右子树之后),并且在遍历左右子树时也遵循同样的规则。本题中,后序遍历序列与中序遍历序列均为 ABCDEF,可确定该二叉树的相结点为F,且每个结点f均不存在右子树,因此按层次输出的序列应为FEDCBA。本题答案为C选项。
A. 15
B. 16
C. 17
D. 不可能有这样的树
解析:解析:假设叶子结点个数为n。度为4的树的总结点数为度为4的结点数+度为3的结点数+度为2的结点数+度为1的结点数+度为0的结点数,即为2+3+1+0+n。再根据树的总的结点数为树中所有结点的度数之和再加1,则总结点数为4×2+3×3+2×3+1×0+0×n+1。4×2+3×3+2×3+1=2+3+3+n,贝h=-16,叶子结点数为16。本题答案为B选项。
A. 10
B. 11
C. 12
D. 不可能有这样的树
解析:解析:假设叶子结点个数为n。树的总结点数为度为3的结点数+度为2的结点数+度为1的结点数+度为O的结点数,即为4+1+3+n。再根据树的总结点数为树中所有结点的度数之和再加1,则总结点数为3×4+2×1+1×3+O×x+1。3×4+2×1+1×3+1=4+1+3+n,则n=10,叶子结点数为10。本题答案为A选项。
A. 该二叉树共有103个结点
B. 该二叉树的结点数不确定
C. 该二叉树共有101个结点
D. 不可能有这样的二叉树
解析:解析:对任何一棵二叉树,度为0的结点(即叶子结点)总是比度为2的结点多一个。本题中,度为2的结点个数为49,则度为O的结点个数为49+1=50。二叉树的总结点数等于度为2的结点数+度为1的结点数+度为0的结点数,则该二叉树的总结点数为49+4+50=103。本题答案为A选项。
A. 该二叉树只能有83个结点
B. 这样的二叉树不惟一
C. 该二叉树共有103个结点
D. 不可能有这样的二叉树
解析:解析:二叉树具有如下性质:对任何一棵二叉树,度为O的结点(即叶子结点〉总是比度为2的结点多一个。本题中,度为2的结点个数为49,度为0的结点个数为30,不符合二叉树的基本性质,不可能有这样的二叉树。本题答案为D选项。
A. 7
B. 8
C. 9
D. 10
解析:解析:二叉树的基本性质:深度为K的二叉树中,最多有2k-1个节点。2?-1<256<2?-1,则该完全二叉树的深度为9。本题答案为C选项。
A. 0
B. 1
C. 2
D. 63
解析:解析:在深度为K的二叉树中,最多有2K-1个结点。该二叉树的深度为7,则该二叉树最多有27-1=127个结点。对任何一棵二叉树,度为0的结点(即叶子结点)总是比度为2的结点多一个。该二叉树中叶子结点个数为64,贝度为2的结点个数为63。假设该二叉树的总结点数为n(n<=127),则度为1的结点数为n-64-63, t最大为127,则度为1的结点个数为0。本题答案为A选项。