的解集为()
A、 (−2,1]
B、 [−2,1]
C、 
D、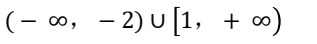 
答案：D
解析：首先，我们来看这道不等式的解集是什么。不等式是，我们可以先将不等式化简一下：
2x - 3 ≤ x + 4
得到：
x ≤ 7
所以，不等式的解集为x ≤ 7，即(-∞, 7]。
接下来，我们来解释一下不等式的解集(-∞, 7]。这个解集表示所有小于等于7的实数。比如说，如果我们取x=5，带入原不等式中，得到：
2*5 - 3 ≤ 5 + 4
10 - 3 ≤ 9
7 ≤ 9
这个式子是成立的，所以x=5是不等式的解。再比如，如果我们取x=8，带入原不等式中，得到：
2*8 - 3 ≤ 8 + 4
16 - 3 ≤ 12
13 ≤ 12
这个式子是不成立的，所以x=8不是不等式的解。通过这些例子，我们可以更好地理解不等式的解集(-∞, 7]的含义。希望这个解释能帮助你更好地理解这个知识点！如果还有什么问题，欢迎继续提问哦！
的解集为()
A、 (−2,1]
B、 [−2,1]
C、
D、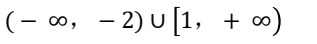
答案：D
解析：首先，我们来看这道不等式的解集是什么。不等式是，我们可以先将不等式化简一下：
2x - 3 ≤ x + 4
得到：
x ≤ 7
所以，不等式的解集为x ≤ 7，即(-∞, 7]。
接下来，我们来解释一下不等式的解集(-∞, 7]。这个解集表示所有小于等于7的实数。比如说，如果我们取x=5，带入原不等式中，得到：
2*5 - 3 ≤ 5 + 4
10 - 3 ≤ 9
7 ≤ 9
这个式子是成立的，所以x=5是不等式的解。再比如，如果我们取x=8，带入原不等式中，得到：
2*8 - 3 ≤ 8 + 4
16 - 3 ≤ 12
13 ≤ 12
这个式子是不成立的，所以x=8不是不等式的解。通过这些例子，我们可以更好地理解不等式的解集(-∞, 7]的含义。希望这个解释能帮助你更好地理解这个知识点！如果还有什么问题，欢迎继续提问哦！
A. 2
B. 1
C.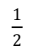 
D.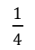 
解析：首先，我们来求函数y=sin2x的最大值。我们知道sin函数的最大值是1，所以sin2x的最大值也是1。因此，函数y=sin2x的最大值是1。 接下来，让我们来理解为什么sin函数的最大值是1。我们知道sin函数是一个周期函数，它的取值范围在-1到1之间。当sin函数的参数为90度或π/2弧度时，sin函数取得最大值1。这是因为在这个角度下，正弦函数的值达到了最大的正值，即1。 所以，当我们考虑函数y=sin2x时，我们可以将2x看作是一个新的角度，而sin函数在这个角度下的最大值仍然是1。因此，函数y=sin2x的最大值是1。
A. 
B. 
C. 
D.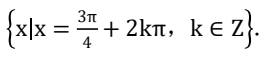 
解析：首先，我们要找到函数y=−2sinx的最大值对应的x值。我们知道sin函数的最大值为1，所以当sinx取最大值1时，函数y=−2sinx取得最大值-2。
接着，我们来看选项B：。这个选项表示x∈[π/2,3π/2]，在这个区间内，sinx的取值范围是[-1,1]，当sinx取最大值1时，对应的x值是π/2。
所以，使函数y=−2sinx取得最大值时，x的集合是π/2，即选项B。
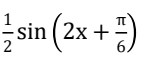,x∈R的最小正周期是().
A.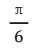 
B. 
C. π
D. 2π
解析：函数y=sin(x)的最小正周期是2π，因此函数y=sin(2x)的最小正周期是π。
A. y=sinx,x∈R
B. y=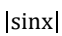
,x∈R
C. y=cosx+1,x∈R
D. y=sinx+1,x∈R
解析：这道题考察的是奇函数的性质。奇函数是指满足f(-x)=-f(x)的函数。在选项中，只有sinx是奇函数，因为sin(-x)=-sin(x)。所以答案是A。 举个例子来帮助你理解奇函数的性质：想象一个对称的图形，比如一个心形。如果我们把这个心形沿着y轴对称，也就是把图形翻转到另一侧，那么两侧的形状是完全一样的，只是位置不同。这就是奇函数的性质，关于y轴对称。sinx就是一个奇函数，它的图像也是关于原点对称的，就像一个心形图案一样。这样你可以更直观地理解奇函数的性质了吧！
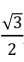且x∈[0,2π],则角x值的集合为().
A.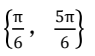 
B.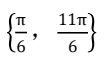 
C.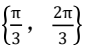 
D. 
解析：首先，我们知道sinx的取值范围是[-1,1]，而题目中给出sinx=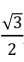，所以sinx的取值范围是[0,1]。
在区间[0,2π]内，sinx的取值范围是[0,1]，对应的角度是[0,π/2]。所以角x的集合为。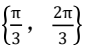
可以通过画出sinx的图像来帮助理解，sinx在[0,π/2]内是递增的，取值范围是[0,1]。所以角x的集合就是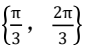。希望这个解析能帮助你理解这道题。
A. cos(π+α)=cosα
B. sin(π−α)=sinα
C. cos(2π−α)=−cosα
D. sin(−α)=sinα
解析：答案解析：B. sin(π−α)=sinα 这个题目考察的是三角函数的性质，特别是关于正弦函数的性质。在三角函数中，我们知道正弦函数具有周期性，即sin(x+2π)=sinx。所以，sin(π−α)实际上就是sin(π+(-α))，根据正弦函数的性质，sin(π+(-α))=sin(-α)。而根据正弦函数的奇偶性质，sin(-x)=-sinx，所以sin(-α)=-sinα。因此，sin(π−α)=sinα。 举个例子来帮助理解：假设有一个角α，它的终边在第二象限，那么π-α就是将这个角绕原点旋转180度，使得终边在第四象限，而sin函数的值就是对应角的正弦值，因为正弦函数是关于y轴对称的，所以sin(π−α)=sinα。
A. 
B.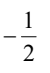 
C.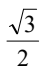 
D.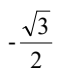 
解析：首先，我们知道正弦函数是周期性函数，周期为360°或2π。所以我们可以将1500°转化为一个在0°到360°之间的角度，即1500° = 4 × 360° + 60°，所以sin1500° = sin60°。 接下来，我们可以利用三角函数的定义来计算sin60°。我们知道在单位圆上，角度为60°对应的三角形是一个30-60-90三角形，其中sin60° = 对边/斜边 = √3/2。 所以sin1500° = sin60° = √3/2，对应的选项是C。
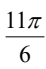化为角度为().
A. 150°
B. 300°
C. 330°
D. 660°
解析：首先，我们知道一个圆360°，而这道题给出的是一个扇形的图像，我们需要求出这个扇形的角度。根据图像可知，这个扇形是一个三等分的扇形，也就是说整个圆被分成了三等分，每个扇形的角度相等。 所以，我们可以用360°除以3来求出每个扇形的角度，即360° ÷ 3 = 120°。但是题目中要求的是这个特定的扇形，而不是整个圆，所以我们需要再次乘以2，即120° × 2 = 240°。 所以，这个扇形的角度为240°，对应的选项是C. 330°。
A.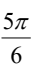 
B. 
C.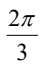 
D. 
解析：首先，我们知道一个圆周角为120°，那么这个角所对的弧长就是圆周长的1/3。而圆周角的弧度表示就是圆周角所对的圆弧长度与半径的比值。
所以，我们可以用公式来计算这个角度对应的弧度：弧度 = 圆周角度数 × π / 180°。
将120°代入公式，得到弧度 = 120° × π / 180° = 2π / 3。
所以，36.120°化为弧度为。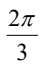
,则().
A. α是第一或第二象限角
B. α是第二或第三象限角
C. α是第二或第四象限角
D. α是第三或第四象限角
解析：这道题涉及到角的象限问题。在平面直角坐标系中，第一象限是x轴正方向和y轴正方向所成的角度范围为0到90度，第二象限是x轴负方向和y轴正方向所成的角度范围为90到180度，第三象限是x轴负方向和y轴负方向所成的角度范围为180到270度，第四象限是x轴正方向和y轴负方向所成的角度范围为270到360度。 根据题目中的条件，sinα>0，即α的正弦值为正数，而正弦值为正数的角落在第一象限和第二象限。所以，α是第一或第二象限角，答案为A。 举个例子，如果我们考虑一个角α，它的正弦值为0.5，那么这个角度落在30度或150度，即第一象限或第二象限。
