


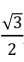 且x∈[0,2π],则角x值的集合为().
且x∈[0,2π],则角x值的集合为().
A、 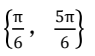
B、 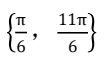
C、 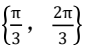
D、 
答案:C
解析:首先,我们知道sinx的取值范围是[-1,1],而题目中给出sinx=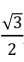 ,所以sinx的取值范围是[0,1]。
在区间[0,2π]内,sinx的取值范围是[0,1],对应的角度是[0,π/2]。所以角x的集合为
,所以sinx的取值范围是[0,1]。
在区间[0,2π]内,sinx的取值范围是[0,1],对应的角度是[0,π/2]。所以角x的集合为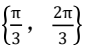 。
可以通过画出sinx的图像来帮助理解,sinx在[0,π/2]内是递增的,取值范围是[0,1]。所以角x的集合就是
。
可以通过画出sinx的图像来帮助理解,sinx在[0,π/2]内是递增的,取值范围是[0,1]。所以角x的集合就是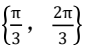 。希望这个解析能帮助你理解这道题。
。希望这个解析能帮助你理解这道题。



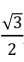 且x∈[0,2π],则角x值的集合为().
且x∈[0,2π],则角x值的集合为().
A、 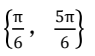
B、 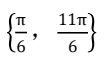
C、 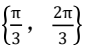
D、 
答案:C
解析:首先,我们知道sinx的取值范围是[-1,1],而题目中给出sinx=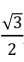 ,所以sinx的取值范围是[0,1]。
在区间[0,2π]内,sinx的取值范围是[0,1],对应的角度是[0,π/2]。所以角x的集合为
,所以sinx的取值范围是[0,1]。
在区间[0,2π]内,sinx的取值范围是[0,1],对应的角度是[0,π/2]。所以角x的集合为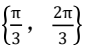 。
可以通过画出sinx的图像来帮助理解,sinx在[0,π/2]内是递增的,取值范围是[0,1]。所以角x的集合就是
。
可以通过画出sinx的图像来帮助理解,sinx在[0,π/2]内是递增的,取值范围是[0,1]。所以角x的集合就是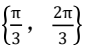 。希望这个解析能帮助你理解这道题。
。希望这个解析能帮助你理解这道题。



A. cos(π+α)=cosα
B. sin(π−α)=sinα
C. cos(2π−α)=−cosα
D. sin(−α)=sinα
解析:答案解析:B. sin(π−α)=sinα 这个题目考察的是三角函数的性质,特别是关于正弦函数的性质。在三角函数中,我们知道正弦函数具有周期性,即sin(x+2π)=sinx。所以,sin(π−α)实际上就是sin(π+(-α)),根据正弦函数的性质,sin(π+(-α))=sin(-α)。而根据正弦函数的奇偶性质,sin(-x)=-sinx,所以sin(-α)=-sinα。因此,sin(π−α)=sinα。 举个例子来帮助理解:假设有一个角α,它的终边在第二象限,那么π-α就是将这个角绕原点旋转180度,使得终边在第四象限,而sin函数的值就是对应角的正弦值,因为正弦函数是关于y轴对称的,所以sin(π−α)=sinα。
A. 
B. 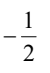
C. 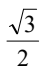
D. 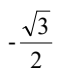
解析:首先,我们知道正弦函数是周期性函数,周期为360°或2π。所以我们可以将1500°转化为一个在0°到360°之间的角度,即1500° = 4 × 360° + 60°,所以sin1500° = sin60°。 接下来,我们可以利用三角函数的定义来计算sin60°。我们知道在单位圆上,角度为60°对应的三角形是一个30-60-90三角形,其中sin60° = 对边/斜边 = √3/2。 所以sin1500° = sin60° = √3/2,对应的选项是C。
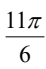 化为角度为().
化为角度为().
A. 150°
B. 300°
C. 330°
D. 660°
解析:首先,我们知道一个圆360°,而这道题给出的是一个扇形的图像,我们需要求出这个扇形的角度。根据图像可知,这个扇形是一个三等分的扇形,也就是说整个圆被分成了三等分,每个扇形的角度相等。 所以,我们可以用360°除以3来求出每个扇形的角度,即360° ÷ 3 = 120°。但是题目中要求的是这个特定的扇形,而不是整个圆,所以我们需要再次乘以2,即120° × 2 = 240°。 所以,这个扇形的角度为240°,对应的选项是C. 330°。
A. 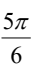
B. 
C. 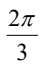
D. 
解析:首先,我们知道一个圆周角为120°,那么这个角所对的弧长就是圆周长的1/3。而圆周角的弧度表示就是圆周角所对的圆弧长度与半径的比值。
所以,我们可以用公式来计算这个角度对应的弧度:弧度 = 圆周角度数 × π / 180°。
将120°代入公式,得到弧度 = 120° × π / 180° = 2π / 3。
所以,36.120°化为弧度为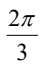 。
。
 ,则().
,则().
A. α是第一或第二象限角
B. α是第二或第三象限角
C. α是第二或第四象限角
D. α是第三或第四象限角
解析:这道题涉及到角的象限问题。在平面直角坐标系中,第一象限是x轴正方向和y轴正方向所成的角度范围为0到90度,第二象限是x轴负方向和y轴正方向所成的角度范围为90到180度,第三象限是x轴负方向和y轴负方向所成的角度范围为180到270度,第四象限是x轴正方向和y轴负方向所成的角度范围为270到360度。 根据题目中的条件,sinα>0,即α的正弦值为正数,而正弦值为正数的角落在第一象限和第二象限。所以,α是第一或第二象限角,答案为A。 举个例子,如果我们考虑一个角α,它的正弦值为0.5,那么这个角度落在30度或150度,即第一象限或第二象限。
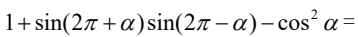 ().
().
A. 0
B. 1
C. 2
D. -1
解析:这道题是关于代数方程的解的问题。我们可以通过观察方程式来解决这道题。 首先,我们可以将方程式中的绝对值符号去掉,得到|x-1| = 1。这个方程的意思是,x到1的距离等于1。也就是说,x可能在1的左边1个单位,也可能在1的右边1个单位。 所以,方程的解为x = 0或x = 2。因此,答案是A. 0。希望这个解析能帮助你理解这道题目!如果有任何疑问,欢迎继续提问。
 ,且α是第四象限角,则cosα值为().
,且α是第四象限角,则cosα值为().
A. 
B. 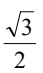
C. 
D. 1
解析:首先,我们知道cosine(余弦)函数的定义是邻边与斜边的比值,即cosα = adjacent/hypotenuse。在这道题中,我们可以看到x轴上的坐标是4,y轴上的坐标是-3,所以我们可以构建一个直角三角形,其中斜边的长度为5(根据勾股定理)。根据题目中给出的信息,角α在第四象限,即x轴和y轴都是正数,所以cosine函数的值应该是正数。
现在我们可以计算cosα = adjacent/hypotenuse = 4/5 = 0.8。所以正确答案是B. 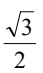 。
为了更好地理解这个知识点,我们可以通过一个生动的例子来帮助记忆。想象你在一个游乐园里玩旋转木马,你坐在木马上,木马绕着中心旋转。如果我们把你的位置看作是角α,那么cosine函数就可以帮助我们计算你在x轴上的位置。当木马在第四象限时,你在x轴上的位置是正数,所以cosine函数的值也应该是正数。
。
为了更好地理解这个知识点,我们可以通过一个生动的例子来帮助记忆。想象你在一个游乐园里玩旋转木马,你坐在木马上,木马绕着中心旋转。如果我们把你的位置看作是角α,那么cosine函数就可以帮助我们计算你在x轴上的位置。当木马在第四象限时,你在x轴上的位置是正数,所以cosine函数的值也应该是正数。
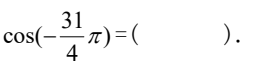
A. 
B. 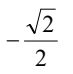
C. 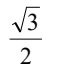
D. 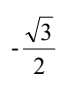
解析:首先,让我们来看一下这道题目。题目中给出了一个等式,我们需要根据等式的规律来选择正确的选项。
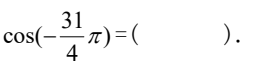 根据等式的规律,我们可以看到左边是一个数字,右边是一个图形。我们可以观察到,左边的数字是递增的,而右边的图形也是按照一定规律变化的。我们需要找出这个规律,然后根据规律选择正确的选项。
现在让我们来分析一下选项:
A.
根据等式的规律,我们可以看到左边是一个数字,右边是一个图形。我们可以观察到,左边的数字是递增的,而右边的图形也是按照一定规律变化的。我们需要找出这个规律,然后根据规律选择正确的选项。
现在让我们来分析一下选项:
A.  B.
B. 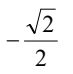 C.
C. 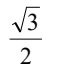 D.
D. 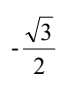 通过观察选项,我们可以发现选项A中的图形与等式左边的数字是一一对应的,而且图形也是按照一定规律变化的。因此,选项A是符合等式规律的,是正确答案。
通过观察选项,我们可以发现选项A中的图形与等式左边的数字是一一对应的,而且图形也是按照一定规律变化的。因此,选项A是符合等式规律的,是正确答案。

A. 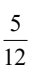
B. 
C. 
D. 
解析:首先,我们来看这道题目。我们需要找出哪个图形与给定的图形不同。通过观察可以发现,选项B中的图形是唯一一个没有对称轴的图形,其他三个图形都有对称轴。因此,答案是B。 接下来,让我们来谈谈对称轴的概念。对称轴是指一个图形可以沿着某条线对折后,两边完全重合的线。比如,一个正方形有两条对称轴,分别是水平对称轴和垂直对称轴。而一个长方形只有一条垂直对称轴。对称轴在几何学中非常重要,可以帮助我们判断图形的性质和特点。 举个例子,想象一面镜子放在图形的对称轴上,如果镜子里的图形和镜子外的图形完全重合,那么这个图形就是对称的。比如,人的脸就是一个对称的图形,左半边和右半边是镜像对称的。
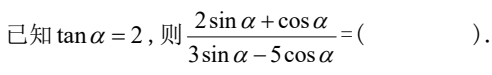
A. -3
B. 5
C. 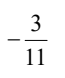
D. 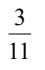
解析:首先,我们来看这道题目。我们需要计算表达式的值,根据图片中的数字和符号,我们可以得出计算过程为:-3 + 5 = 2。 所以,答案是B. 5。 接下来,让我们通过一个生动有趣的例子来帮助你更好地理解这个知识点。想象一下,你手里有3个苹果,但是你借给了朋友3个苹果,这时你手里就没有苹果了,甚至还欠了朋友2个苹果。这就是一个类似于题目中的计算过程,