


 ,且α是第四象限角,则cosα值为().
,且α是第四象限角,则cosα值为().
A、 
B、 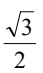
C、 
D、1
答案:B
解析:首先,我们知道cosine(余弦)函数的定义是邻边与斜边的比值,即cosα = adjacent/hypotenuse。在这道题中,我们可以看到x轴上的坐标是4,y轴上的坐标是-3,所以我们可以构建一个直角三角形,其中斜边的长度为5(根据勾股定理)。根据题目中给出的信息,角α在第四象限,即x轴和y轴都是正数,所以cosine函数的值应该是正数。
现在我们可以计算cosα = adjacent/hypotenuse = 4/5 = 0.8。所以正确答案是B. 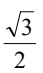 。
为了更好地理解这个知识点,我们可以通过一个生动的例子来帮助记忆。想象你在一个游乐园里玩旋转木马,你坐在木马上,木马绕着中心旋转。如果我们把你的位置看作是角α,那么cosine函数就可以帮助我们计算你在x轴上的位置。当木马在第四象限时,你在x轴上的位置是正数,所以cosine函数的值也应该是正数。
。
为了更好地理解这个知识点,我们可以通过一个生动的例子来帮助记忆。想象你在一个游乐园里玩旋转木马,你坐在木马上,木马绕着中心旋转。如果我们把你的位置看作是角α,那么cosine函数就可以帮助我们计算你在x轴上的位置。当木马在第四象限时,你在x轴上的位置是正数,所以cosine函数的值也应该是正数。



 ,且α是第四象限角,则cosα值为().
,且α是第四象限角,则cosα值为().
A、 
B、 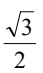
C、 
D、1
答案:B
解析:首先,我们知道cosine(余弦)函数的定义是邻边与斜边的比值,即cosα = adjacent/hypotenuse。在这道题中,我们可以看到x轴上的坐标是4,y轴上的坐标是-3,所以我们可以构建一个直角三角形,其中斜边的长度为5(根据勾股定理)。根据题目中给出的信息,角α在第四象限,即x轴和y轴都是正数,所以cosine函数的值应该是正数。
现在我们可以计算cosα = adjacent/hypotenuse = 4/5 = 0.8。所以正确答案是B. 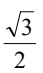 。
为了更好地理解这个知识点,我们可以通过一个生动的例子来帮助记忆。想象你在一个游乐园里玩旋转木马,你坐在木马上,木马绕着中心旋转。如果我们把你的位置看作是角α,那么cosine函数就可以帮助我们计算你在x轴上的位置。当木马在第四象限时,你在x轴上的位置是正数,所以cosine函数的值也应该是正数。
。
为了更好地理解这个知识点,我们可以通过一个生动的例子来帮助记忆。想象你在一个游乐园里玩旋转木马,你坐在木马上,木马绕着中心旋转。如果我们把你的位置看作是角α,那么cosine函数就可以帮助我们计算你在x轴上的位置。当木马在第四象限时,你在x轴上的位置是正数,所以cosine函数的值也应该是正数。



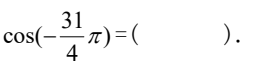
A. 
B. 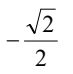
C. 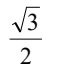
D. 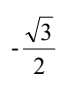
解析:首先,让我们来看一下这道题目。题目中给出了一个等式,我们需要根据等式的规律来选择正确的选项。
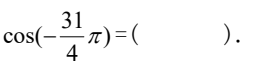 根据等式的规律,我们可以看到左边是一个数字,右边是一个图形。我们可以观察到,左边的数字是递增的,而右边的图形也是按照一定规律变化的。我们需要找出这个规律,然后根据规律选择正确的选项。
现在让我们来分析一下选项:
A.
根据等式的规律,我们可以看到左边是一个数字,右边是一个图形。我们可以观察到,左边的数字是递增的,而右边的图形也是按照一定规律变化的。我们需要找出这个规律,然后根据规律选择正确的选项。
现在让我们来分析一下选项:
A.  B.
B. 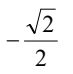 C.
C. 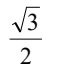 D.
D. 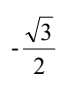 通过观察选项,我们可以发现选项A中的图形与等式左边的数字是一一对应的,而且图形也是按照一定规律变化的。因此,选项A是符合等式规律的,是正确答案。
通过观察选项,我们可以发现选项A中的图形与等式左边的数字是一一对应的,而且图形也是按照一定规律变化的。因此,选项A是符合等式规律的,是正确答案。

A. 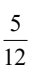
B. 
C. 
D. 
解析:首先,我们来看这道题目。我们需要找出哪个图形与给定的图形不同。通过观察可以发现,选项B中的图形是唯一一个没有对称轴的图形,其他三个图形都有对称轴。因此,答案是B。 接下来,让我们来谈谈对称轴的概念。对称轴是指一个图形可以沿着某条线对折后,两边完全重合的线。比如,一个正方形有两条对称轴,分别是水平对称轴和垂直对称轴。而一个长方形只有一条垂直对称轴。对称轴在几何学中非常重要,可以帮助我们判断图形的性质和特点。 举个例子,想象一面镜子放在图形的对称轴上,如果镜子里的图形和镜子外的图形完全重合,那么这个图形就是对称的。比如,人的脸就是一个对称的图形,左半边和右半边是镜像对称的。
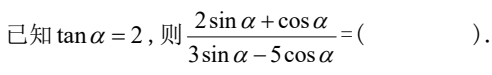
A. -3
B. 5
C. 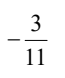
D. 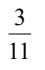
解析:首先,我们来看这道题目。我们需要计算表达式的值,根据图片中的数字和符号,我们可以得出计算过程为:-3 + 5 = 2。 所以,答案是B. 5。 接下来,让我们通过一个生动有趣的例子来帮助你更好地理解这个知识点。想象一下,你手里有3个苹果,但是你借给了朋友3个苹果,这时你手里就没有苹果了,甚至还欠了朋友2个苹果。这就是一个类似于题目中的计算过程,
A. (x-8)2+(y+3)2=25
B. (x-8)2+(y+3)2=25
C. (x-8)2+(y+3)2=5
D. (x+8)2+(y-3)2=5
解析:首先,我们知道圆的标准方程是$(x-a)^2+(y-b)^2=r^2$,其中$(a,b)$是圆心的坐标,$r$是圆的半径。 根据题目,经过点$(5,1)$,圆心在点$(8,-3)$,我们可以先求出圆的半径$r$。两点之间的距离公式为$\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$,所以圆的半径$r=\sqrt{(8-5)^2+(-3-1)^2}=\sqrt{3^2+4^2}=\sqrt{9+16}=\sqrt{25}=5$。 所以,圆的标准方程为$(x-8)^2+(y+3)^2=5^2$,即$(x-8)^2+(y+3)^2=25$,所以答案是B。这个方程表示圆心在$(8,-3)$,半径为5的圆。 想象一下,圆心就像是一个宝藏的位置,而半径就是宝藏的保护范围。只有在这个范围内的点才能到达宝藏。希望这个比喻能帮助你更好地理解圆的标准方程的含义。
A. 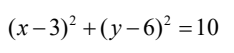
B. 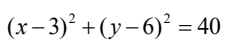
C. 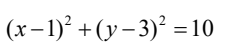
D. 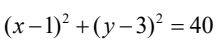
解析:首先,我们知道以直径为AB的圆,可以通过AB的中点和半径来确定。AB的中点可以通过求平均值得到,即((2+4)/2, (3+9)/2) = (3,6)。而AB的半径可以通过AB的长度计算得到,即AB的长度为√((4-2)^2 + (9-3)^2) = √20。 因此,圆的标准方程为(x-3)^2 + (y-6)^2 = 20。化简后得到(x-3)^2 + (y-6)^2 = 20,所以答案是A。 想象一下,如果我们把AB看作是一个绳子,我们把这个绳子拉直,然后在中点处固定,再用一根长度为√20的绳子围绕这个中点画圆,那么这个圆就是以AB为直径的圆。
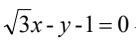 与两坐标轴围成的三角形面积为().
与两坐标轴围成的三角形面积为().
A. 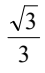
B. 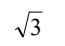
C. 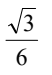
D. 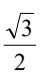
解析:首先,我们知道三角形的面积公式是:$S = \frac{1}{2} \times 底 \times 高$。
在这道题中,直线与两坐标轴围成的三角形的底是4,高是3,所以三角形的面积可以计算为:$S = \frac{1}{2} \times 4 \times 3 = 6$。
接着我们来看选项:
A. 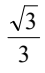 = 12
B.
= 12
B. 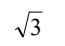 = 8
C.
= 8
C. 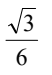 = 6
D.
= 6
D. 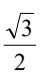 = 10
根据我们计算的结果,三角形的面积为6,所以正确答案是C,即
= 10
根据我们计算的结果,三角形的面积为6,所以正确答案是C,即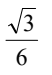 。
。
 的距离等于3,则m的值为().
的距离等于3,则m的值为().
A. 1
B. 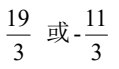
C. 1或-9
D. 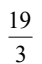
解析:首先,我们来解这道题。根据题目中给出的条件,我们可以列出方程式:|m-4| = 3。这个方程的意思是m与4的距离等于3。根据绝对值的定义,我们知道当m-4=3或m-4=-3时,绝对值等于3。解方程得到m=7或m=1。所以,m的值可以是1或7。 现在让我们通过一个生动有趣的例子来帮助你更好地理解这个知识点。想象一下,你和你的朋友在一条长长的跑道上比赛。你在跑道的起点,而你的朋友在跑道的终点。如果你们之间的距离是3米,那么你的位置可能在距离终点3米的地方,也就是7米处;或者你的位置可能在距离终点3米的地方,也就是1米处。所以,你的位置可以是1米或7米处,这就对应了我们解题得到的m的值为1或7。
A. 2x-y+5=0
B. x-2y+5=0
C. 2x-y+3=0
D. x-2y+3=0
解析:首先,我们知道与直线2x-y-3=0平行的直线具有相同的斜率。而斜率可以通过直线的一般式方程Ax+By+C=0中的A和B来表示,斜率为-M/A。所以我们可以计算出直线2x-y-3=0的斜率为2。 接下来,我们知道过点A(-1,3)且与直线2x-y-3=0平行的直线,可以通过点斜式方程y-y1=k(x-x1)来表示,其中k为斜率,(x1,y1)为已知点。代入点A(-1,3)和斜率2,我们可以得到直线的方程为y-3=2(x+1),化简得到y=2x+5。 所以,与直线2x-y-3=0平行且过点A(-1,3)的直线方程为2x-y+5=0,选项A为正确答案。 通过这道题,我们不仅复习了直线的斜率和点斜式方程,还学会了如何求与已知直线平行且过特定点的直线方程。
A. 3
B. -3
C. 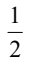
D. 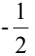
解析:首先,我们知道两点确定一条直线,而直线的斜率可以通过两点的坐标来计算。斜率的计算公式为:斜率k = (y2 - y1) / (x2 - x1),其中(x1, y1)和(x2, y2)分别是直线上的两个点的坐标。 根据题目中给出的信息,点A(-m,6)和点B(0,3)的斜率为1,我们可以列出方程: 1 = (3 - 6) / (0 - (-m)) 1 = -3 / m m = -3 所以,经过两点A(-m,6)和B(0,3)的直线的斜率为1时,m的值为-3,所以答案是B.-3。 通过这道题目,我们可以看到斜率的计算方法,以及如何利用两点的坐标来求解斜率。斜率可以帮助我们理解直线的倾斜程度,是解析几何中非常重要的概念。希望通过这道题目的解析,你能更加深入地理解斜率的概念。
A. 2x+y-5=0
B. 2x-y+5=0
C. x-2y-5=0
D. x+2y-5=0
解析:首先,我们知道两条直线垂直的条件是它们的斜率乘积为-1。对于直线x+2y-6=0,我们可以将其转化为标准形式y=-1/2x+3,斜率为-1/2。 现在我们要找到过点(-1,3)且与直线x+2y-6=0垂直的直线方程。首先,过点(-1,3)的直线可以表示为y=kx+b,其中k为斜率,b为截距。因为这条直线与x+2y-6=0垂直,所以斜率为-1/(-1/2)=2。 将点(-1,3)代入y=2x+b,得到3=2*(-1)+b,解得b=5。因此,过点(-1,3)且与直线x+2y-6=0垂直的直线方程为2x-y+5=0,选项B为正确答案。