


A、 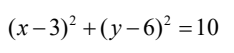
B、 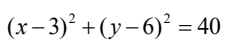
C、 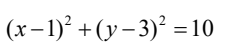
D、 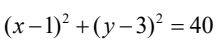
答案:A
解析:首先,我们知道以直径为AB的圆,可以通过AB的中点和半径来确定。AB的中点可以通过求平均值得到,即((2+4)/2, (3+9)/2) = (3,6)。而AB的半径可以通过AB的长度计算得到,即AB的长度为√((4-2)^2 + (9-3)^2) = √20。 因此,圆的标准方程为(x-3)^2 + (y-6)^2 = 20。化简后得到(x-3)^2 + (y-6)^2 = 20,所以答案是A。 想象一下,如果我们把AB看作是一个绳子,我们把这个绳子拉直,然后在中点处固定,再用一根长度为√20的绳子围绕这个中点画圆,那么这个圆就是以AB为直径的圆。



A、 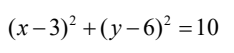
B、 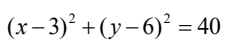
C、 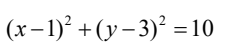
D、 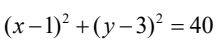
答案:A
解析:首先,我们知道以直径为AB的圆,可以通过AB的中点和半径来确定。AB的中点可以通过求平均值得到,即((2+4)/2, (3+9)/2) = (3,6)。而AB的半径可以通过AB的长度计算得到,即AB的长度为√((4-2)^2 + (9-3)^2) = √20。 因此,圆的标准方程为(x-3)^2 + (y-6)^2 = 20。化简后得到(x-3)^2 + (y-6)^2 = 20,所以答案是A。 想象一下,如果我们把AB看作是一个绳子,我们把这个绳子拉直,然后在中点处固定,再用一根长度为√20的绳子围绕这个中点画圆,那么这个圆就是以AB为直径的圆。



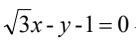 与两坐标轴围成的三角形面积为().
与两坐标轴围成的三角形面积为().
A. 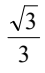
B. 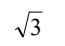
C. 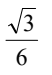
D. 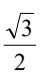
解析:首先,我们知道三角形的面积公式是:$S = \frac{1}{2} \times 底 \times 高$。
在这道题中,直线与两坐标轴围成的三角形的底是4,高是3,所以三角形的面积可以计算为:$S = \frac{1}{2} \times 4 \times 3 = 6$。
接着我们来看选项:
A. 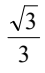 = 12
B.
= 12
B. 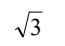 = 8
C.
= 8
C. 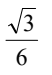 = 6
D.
= 6
D. 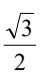 = 10
根据我们计算的结果,三角形的面积为6,所以正确答案是C,即
= 10
根据我们计算的结果,三角形的面积为6,所以正确答案是C,即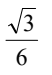 。
。
 的距离等于3,则m的值为().
的距离等于3,则m的值为().
A. 1
B. 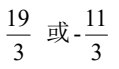
C. 1或-9
D. 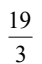
解析:首先,我们来解这道题。根据题目中给出的条件,我们可以列出方程式:|m-4| = 3。这个方程的意思是m与4的距离等于3。根据绝对值的定义,我们知道当m-4=3或m-4=-3时,绝对值等于3。解方程得到m=7或m=1。所以,m的值可以是1或7。 现在让我们通过一个生动有趣的例子来帮助你更好地理解这个知识点。想象一下,你和你的朋友在一条长长的跑道上比赛。你在跑道的起点,而你的朋友在跑道的终点。如果你们之间的距离是3米,那么你的位置可能在距离终点3米的地方,也就是7米处;或者你的位置可能在距离终点3米的地方,也就是1米处。所以,你的位置可以是1米或7米处,这就对应了我们解题得到的m的值为1或7。
A. 2x-y+5=0
B. x-2y+5=0
C. 2x-y+3=0
D. x-2y+3=0
解析:首先,我们知道与直线2x-y-3=0平行的直线具有相同的斜率。而斜率可以通过直线的一般式方程Ax+By+C=0中的A和B来表示,斜率为-M/A。所以我们可以计算出直线2x-y-3=0的斜率为2。 接下来,我们知道过点A(-1,3)且与直线2x-y-3=0平行的直线,可以通过点斜式方程y-y1=k(x-x1)来表示,其中k为斜率,(x1,y1)为已知点。代入点A(-1,3)和斜率2,我们可以得到直线的方程为y-3=2(x+1),化简得到y=2x+5。 所以,与直线2x-y-3=0平行且过点A(-1,3)的直线方程为2x-y+5=0,选项A为正确答案。 通过这道题,我们不仅复习了直线的斜率和点斜式方程,还学会了如何求与已知直线平行且过特定点的直线方程。
A. 3
B. -3
C. 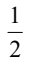
D. 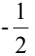
解析:首先,我们知道两点确定一条直线,而直线的斜率可以通过两点的坐标来计算。斜率的计算公式为:斜率k = (y2 - y1) / (x2 - x1),其中(x1, y1)和(x2, y2)分别是直线上的两个点的坐标。 根据题目中给出的信息,点A(-m,6)和点B(0,3)的斜率为1,我们可以列出方程: 1 = (3 - 6) / (0 - (-m)) 1 = -3 / m m = -3 所以,经过两点A(-m,6)和B(0,3)的直线的斜率为1时,m的值为-3,所以答案是B.-3。 通过这道题目,我们可以看到斜率的计算方法,以及如何利用两点的坐标来求解斜率。斜率可以帮助我们理解直线的倾斜程度,是解析几何中非常重要的概念。希望通过这道题目的解析,你能更加深入地理解斜率的概念。
A. 2x+y-5=0
B. 2x-y+5=0
C. x-2y-5=0
D. x+2y-5=0
解析:首先,我们知道两条直线垂直的条件是它们的斜率乘积为-1。对于直线x+2y-6=0,我们可以将其转化为标准形式y=-1/2x+3,斜率为-1/2。 现在我们要找到过点(-1,3)且与直线x+2y-6=0垂直的直线方程。首先,过点(-1,3)的直线可以表示为y=kx+b,其中k为斜率,b为截距。因为这条直线与x+2y-6=0垂直,所以斜率为-1/(-1/2)=2。 将点(-1,3)代入y=2x+b,得到3=2*(-1)+b,解得b=5。因此,过点(-1,3)且与直线x+2y-6=0垂直的直线方程为2x-y+5=0,选项B为正确答案。
A. 2
B. 3
C. -2
D. -3
解析:首先,我们知道两条直线垂直的条件是它们的斜率的乘积为-1。两条直线的斜率分别为-a/2 和 2/3。所以我们可以得到方程:(-a/2) * (2/3) = -1,解得a=3。 可以这样理解:两条直线垂直的时候,它们的斜率的乘积为-1,就好比两条相互垂直的墙壁,一个墙壁的倾斜程度(斜率)为a/2,另一个墙壁的倾斜程度为2/3,它们的乘积为-1,这样两面墙壁才能够互相垂直。所以在这道题中,a=3。
A. 4,-3
B. -4,-12
C. 6,12
D. 8,-12
解析:首先,我们知道点P(4,9)是线段AB的中点,即P是线段AB的中间点,所以P的横坐标和纵坐标分别是A和B的横坐标和纵坐标的平均值。 根据题目中给出的信息,点A的坐标是(m,6),点B的坐标是(0,-n),点P的坐标是(4,9)。 根据中点的性质,我们可以列出以下两个方程: (4+m)/2 = 4 --> 4+m = 8 --> m = 4 (6-n)/2 = 9 --> 6-n = 18 --> n = -12 所以,m的值为4,n的值为-12,所以答案为D. 8,-12。 为了更好地理解中点的概念,我们可以想象一条线段上有两个点A和B,点P是这条线段上的一个点,且P是AB的中点。这就好像我们在一根绳子上找到中间点一样,这个中点将绳子分成了两段长度相等的部分。
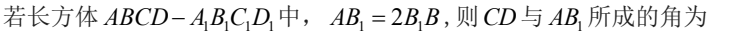 ().
().
A. 30°
B. 45°
C. 60°
D. 90°
解析:这道题是关于三角形内角和的问题。根据三角形内角和的性质,三角形的三个内角之和总是180°。在这道题中,已知两个角分别为30°和60°,我们需要求出第三个角的度数。 设第三个角的度数为x°,根据三角形内角和的性质,可以列出方程:30° + 60° + x° = 180°。 解方程得:x° = 180° - 30° - 60° = 90°。 因此,第三个角的度数为90°,所以答案是A. 30°。 可以通过想象一个直角三角形来帮助理解:直角三角形的两个锐角分别为30°和60°,而直角三角形的直角为90°,所以第三个角的度数为90°。
A. 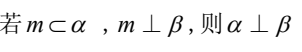
B. 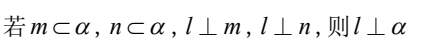
C. 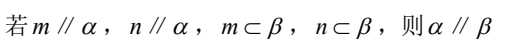
D. 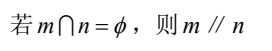
解析:首先,我们来看一下这道题目中的四个命题。在数学中,我们知道一个命题是一个陈述句,可以被判断为真或假。在这道题目中,我们需要判断哪一个命题是正确的。
A. 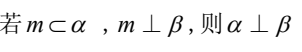 这个命题是一个等式,左边是一个分式,右边是一个整数。我们可以通过计算来验证这个等式是否成立。
B.
这个命题是一个等式,左边是一个分式,右边是一个整数。我们可以通过计算来验证这个等式是否成立。
B. 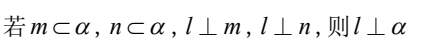 这个命题是一个不等式,左边是一个分式,右边是一个整数。我们可以通过计算来验证这个不等式是否成立。
C.
这个命题是一个不等式,左边是一个分式,右边是一个整数。我们可以通过计算来验证这个不等式是否成立。
C. 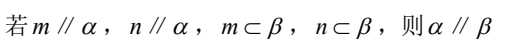 这个命题是一个等式,左边是一个分式,右边是一个整数。我们可以通过计算来验证这个等式是否成立。
D.
这个命题是一个等式,左边是一个分式,右边是一个整数。我们可以通过计算来验证这个等式是否成立。
D. 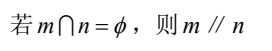 这个命题是一个不等式,左边是一个分式,右边是一个整数。我们可以通过计算来验证这个不等式是否成立。
通过计算我们可以得出,只有命题A是正确的,因此答案是A。
这个命题是一个不等式,左边是一个分式,右边是一个整数。我们可以通过计算来验证这个不等式是否成立。
通过计算我们可以得出,只有命题A是正确的,因此答案是A。
A. 3
B. 6
C. 9
D. 27
解析:首先,我们可以设小球的半径为r,大球的半径为3r。 小球的表面积为4πr^2,大球的表面积为4π(3r)^2=36πr^2。 所以,大球表面积是小球表面积的36πr^2/4πr^2=9倍。 所以答案是C,大球表面积是小球表面积的9倍。 可以这样联想,如果我们把一个小球放大3倍,那么它的表面积会变成原来的9倍。就像我们把一个小苹果放大成一个大苹果,大苹果的表面积就是小苹果的9倍一样。