


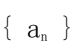 中,a1=2,a7=20,则S7=().
中,a1=2,a7=20,则S7=().
A、14
B、22
C、70
D、77
答案:D
解析:首先,我们知道等差数列是指一个数列中任意相邻两项的差都相等的数列。在这道题中,我们已知a1=2,a7=20,我们需要求出S7,即数列的前7项和。 根据等差数列的性质,我们可以得到a7=a1+6d,其中d为公差。将已知的a1=2和a7=20代入,得到20=2+6d,解方程得到d=3。 接下来,我们可以利用等差数列的求和公式来求解S7。等差数列的前n项和公式为Sn=n(a1+an)/2,其中n为项数,a1为首项,an为末项。 将n=7,a1=2,an=20代入公式,得到S7=7(2+20)/2=77。 因此,答案为D. 77。



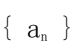 中,a1=2,a7=20,则S7=().
中,a1=2,a7=20,则S7=().
A、14
B、22
C、70
D、77
答案:D
解析:首先,我们知道等差数列是指一个数列中任意相邻两项的差都相等的数列。在这道题中,我们已知a1=2,a7=20,我们需要求出S7,即数列的前7项和。 根据等差数列的性质,我们可以得到a7=a1+6d,其中d为公差。将已知的a1=2和a7=20代入,得到20=2+6d,解方程得到d=3。 接下来,我们可以利用等差数列的求和公式来求解S7。等差数列的前n项和公式为Sn=n(a1+an)/2,其中n为项数,a1为首项,an为末项。 将n=7,a1=2,an=20代入公式,得到S7=7(2+20)/2=77。 因此,答案为D. 77。



A. 2
B. 3
C. 4
D. 6
解析:首先,我们知道等差数列是指相邻两项之间的差值都相等的数列。在这道题中,我们已知等差数列的第1项是7,第9项是1。 我们可以利用等差数列的通项公式来解决这道题。等差数列的通项公式为:$a_n = a_1 + (n-1)d$,其中$a_n$表示第n项,$a_1$表示第1项,d表示公差。 根据题目,我们可以列出两个方程: $a_1 = 7$ $a_9 = 1$ 将这两个方程带入通项公式,我们可以得到: $7 + (9-1)d = 1$ 解方程得到公差d为-1。现在我们可以求得等差数列的第5项: $a_5 = 7 + (5-1)(-1) = 7 + 4(-1) = 7 - 4 = 3$ 所以,等差数列的第5项是3。答案是B. 3。
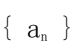 中,a1=4,q=-2,则S3=().
中,a1=4,q=-2,则S3=().
A. 11
B. 12
C. 13
D. 14
解析:首先,我们知道等比数列的通项公式为an = a1 * q^(n-1),其中a1为首项,q为公比,n为项数。 根据题目中的信息,a1=4,q=-2。我们要求S3,即前三项的和。 S3 = a1 + a2 + a3 S3 = 4 + 4*(-2) + 4*(-2)^2 S3 = 4 - 8 + 16 S3 = 12 所以,S3 = 12,选项B为正确答案。 接下来,让我们通过一个生动有趣的例子来理解等比数列。假设有一只兔子,它每个月生一只小兔子,新生的小兔子也会在第二个月开始生小兔子。如果初始时只有一对兔子,第一个月有1对兔子,第二个月有2对兔子,第三个月有4对兔子,第四个月有8对兔子,以此类推。 这个情况就可以用等比数列来表示,首项为1,公比为2。我们可以通过等比数列的求和公式来计算任意月份的兔子总数。这样,我们就可以更好地理解等比数列的应用和意义。
A. n2
B. n(n+1)
C. 
D. 2n2
解析:首先,我们来看一下这道题目。题目要求我们计算前n个正整数的和,我们知道前n个正整数是从1开始的,依次为1, 2, 3, ..., n。那么它们的和可以表示为1 + 2 + 3 + ... + n。 这里我们可以利用数学归纳法来求解这个和。首先我们来看一下前几个正整数的和: 当n=1时,和为1; 当n=2时,和为1+2=3; 当n=3时,和为1+2+3=6; ... 我们可以发现,前n个正整数的和可以表示为n(n+1)/2。所以答案是C选项。 现在让我们通过一个生动有趣的例子来帮助你更好地理解这个知识点。假设有一个小朋友,他有一堆糖果,每天都会吃掉一颗糖果。第一天他吃掉1颗糖果,第二天他吃掉2颗糖果,第三天他吃掉3颗糖果,以此类推。现在我们想知道,经过n天后,他一共吃掉了多少颗糖果呢? 我们可以用前n个正整数的和来表示这个问题。第一天吃1颗,第二天吃2颗,第三天吃3颗,依次类推,经过n天后,他一共吃掉的糖果数就是前n个正整数的和,即n(n+1)/2。这样你就可以更直观地理解这个知识点了。
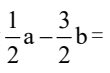 ().
().
A. (-2,-1)
B. (-2,1)
C. (-1,0)
D. (-1,2)
解析:首先,我们知道两个向量相加就是将它们的对应分量相加。所以,我们可以将向量c表示为a+b,即c=(1,1)+(1,-1)=(1+1,1+(-1))=(2,0)。 所以,向量c=(2,0)。在选项中,只有D. (-1,2)符合这个结果,所以答案是D. (-1,2)。 让我们通过一个生动有趣的例子来理解这个知识点:假设向量a代表一个人向东走了1步,向北走了1步,向量b代表这个人向东走了1步,向南走了1步。那么向量c就代表这个人最终的位移,即向东走了2步,向南北方向上的位移抵消了,所以向量c=(2,0)。
A. 22
B. 7
C. -2
D. -15
解析:首先,我们来计算向量a和向量b的点积(内积)。 向量a=(2,-3),向量b=(5,-4)。 a·b = 2*5 + (-3)*(-4) = 10 + 12 = 22。 所以,a·b=22。 点积的计算方法就是将两个向量对应分量相乘再相加起来。 举个生动的例子来帮助理解,假设向量a代表一个人的步长和方向,向量b代表风的速度和方向。那么a·b就代表这个人在这个风的作用下前进的速度,如果a·b为正数,那么这个人会更快地前进;如果a·b为负数,那么这个人会受到风的阻碍,速度会减慢。
A. 1
B. 4
C. 9
D. 12
解析:首先,题目中给出了向量a=(3,m)和b=(2,6),并且已知a与b平行。两个向量平行意味着它们的方向相同或相反,但长度可以不同。 根据题意,向量a与向量b平行,所以它们的方向相同。两个向量平行时,它们的对应分量之比相等。即,3/2 = m/6。解方程得到m=9。 因此,答案是C. 9。 举个生动的例子来帮助理解:想象你在一条笔直的道路上行走,向前走了3步,然后向右转90度,再走m步,这个向量就是a。另一条笔直的道路上有人向前走了2步,然后向右转90度,再走6步,这个向量就是b。由于a与b平行,所以你和那个人的方向是一样的,只是长度不同。根据题目条件,我们可以求出你走的步数m为9步。
A. 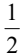
B. 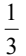
C. 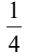
D. 1
解析:这道题是关于概率的计算。在抛硬币的情况下,每次抛硬币出现正面的概率是1/2,出现反面的概率也是1/2。 现在我们要计算抛两次硬币得到两次正面朝上的概率。第一次抛硬币正面朝上的概率是1/2,第二次抛硬币正面朝上的概率也是1/2。因为两次事件是独立的,所以我们可以将两次事件的概率相乘来得到两次正面朝上的概率。 所以,答案是C,即1/2 * 1/2 = 1/4。也就是说,抛两次硬币得到两次正面朝上的概率是1/4。 举个例子来帮助理解:假设你有一枚硬币,你抛两次硬币,想要两次都是正面朝上。第一次抛硬币,正面朝上的概率是1/2,第二次抛硬币,正面朝上的概率也是1/2。所以两次都是正面朝上的概率就是1/2 * 1/2 = 1/4。
A. 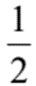
B. 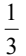
C. 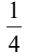
D. 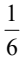
解析:首先,我们来计算一下掷1枚骰子点数不小于4点的情况。一枚普通的骰子有6个面,点数分别为1、2、3、4、5、6。点数不小于4的情况有3种,即4、5、6。所以点数不小于4的概率为3/6=1/2。 现在我们来解释一下为什么答案是A。在选项A中,我们看到了一个骰子的图片,其中有4个面,分别是4、5、6和一个空白的面。这个图片代表了点数不小于4的情况,所以答案是A。
A. 总体
B. 样本
C. 个体
D. 样本容量
解析:这道题涉及到统计学中的样本和总体的概念。在这个问题中,我们调查了一年级学生的体重情况,随机抽取了100个学生进行称重。这100个学生的体重就是我们所称之为样本。 样本是从总体中抽取出来的一部分,用来代表总体特征。在这个例子中,总体是所有一年级学生的体重情况,而我们抽取的100个学生就是样本,用来推断总体的特征。 举个生动的例子,假设你有一个大桶装满了各种颜色的糖果,你想知道这桶糖果的平均颜色是什么。为了节约时间和精力,你可以从桶中随机抽取一小部分糖果,比如10颗,来代表整个桶里的糖果颜色。这里的10颗糖果就是样本,而整个桶里的所有糖果就是总体。 因此,答案是B. 样本。
A. 3件都是正品
B. 至少有1件是正品
C. 3件都是次品
D. 至少有1件是次品
解析:首先,我们来分析一下这道题。已知12件同类产品中,有10件是正品,2件是次品。我们要从中任意抽取3件,问哪种情况是必然事件。 如果我们抽取的3件中至少有1件是正品,那么必然事件就是B选项:至少有1件是正品。因为在12件产品中,有10件是正品,只有2件是次品,所以我们抽取3件时,至少会有1件是正品。这是因为正品的数量比次品多,所以抽取到正品的概率更高。 举个例子来帮助理解:假设我们有12个苹果,其中10个是红苹果,2个是绿苹果。现在我们要从中随机选3个苹果,问至少有1个是红苹果的情况是必然事件还是不可能事件?显然,因为红苹果的数量多,所以在抽取3个苹果时,至少会有1个是红苹果,这是必然事件。