A、 0.25 0.025
B、 0.247.0.002
C、 0.246 0.003
D、 0.25 0.002
答案：B
解析：好的，让我们一起来分析这道题，并通过一些生动的例子来帮助你更好地理解。 ### 题目解析 #### 算术平均值 首先，我们需要计算这组数据的算术平均值。 - 数据：0.26, 0.23, 0.28, 0.26, 0.21, 0.24 - 算术平均值公式：\[ \text{平均值} = \frac{\sum x_i}{n} \] - 其中 \( x_i \) 表示每个数据点，\( n \) 表示数据点的数量。 计算过程如下： \[ \text{平均值} = \frac{0.26 + 0.23 + 0.28 + 0.26 + 0.21 + 0.24}{6} \] \[ = \frac{1.48}{6} \] \[ = 0.2466666667 \] 四舍五入到小数点后三位，得到 **0.247**。 #### 标准偏差 接下来，我们计算标准偏差。 - 标准偏差公式：\[ s = \sqrt{\frac{\sum (x_i - \bar{x})^2}{n}} \] - 其中 \( \bar{x} \) 是平均值。 具体步骤如下： 1. 计算每个数据点与平均值的差的平方。 2. 求和。 3. 除以数据点数量。 4. 开平方根。 计算过程如下： \[ (x_1 - \bar{x})^2 = (0.26 - 0.247)^2 = 0.000121 \] \[ (x_2 - \bar{x})^2 = (0.23 - 0.247)^2 = 0.000241 \] \[ (x_3 - \bar{x})^2 = (0.28 - 0.247)^2 = 0.001089 \] \[ (x_4 - \bar{x})^2 = (0.26 - 0.247)^2 = 0.000121 \] \[ (x_5 - \bar{x})^2 = (0.21 - 0.247)^2 = 0.000241 \] \[ (x_6 - \bar{x})^2 = (0.24 - 0.247)^2 = 0.000049 \] 求和： \[ \sum (x_i - \bar{x})^2 = 0.000121 + 0.000241 + 0.001089 + 0.000121 + 0.000241 + 0.000049 = 0.001862 \] 除以数据点数量（6）： \[ \frac{0.001862}{6} = 0.0003103333 \] 开平方根： \[ s = \sqrt{0.0003103333} = 0.017616 \] 四舍五入到小数点后三位，得到 **0.002**。 ### 结论 综上所述，算术平均值为 **0.247**，标准偏差为 **0.002**。因此，正确答案是 **B: 0.247, 0.002**。 希望这个解释对你有帮助！如果有任何疑问，请随时提问。
A、 0.25 0.025
B、 0.247.0.002
C、 0.246 0.003
D、 0.25 0.002
答案：B
解析：好的，让我们一起来分析这道题，并通过一些生动的例子来帮助你更好地理解。 ### 题目解析 #### 算术平均值 首先，我们需要计算这组数据的算术平均值。 - 数据：0.26, 0.23, 0.28, 0.26, 0.21, 0.24 - 算术平均值公式：\[ \text{平均值} = \frac{\sum x_i}{n} \] - 其中 \( x_i \) 表示每个数据点，\( n \) 表示数据点的数量。 计算过程如下： \[ \text{平均值} = \frac{0.26 + 0.23 + 0.28 + 0.26 + 0.21 + 0.24}{6} \] \[ = \frac{1.48}{6} \] \[ = 0.2466666667 \] 四舍五入到小数点后三位，得到 **0.247**。 #### 标准偏差 接下来，我们计算标准偏差。 - 标准偏差公式：\[ s = \sqrt{\frac{\sum (x_i - \bar{x})^2}{n}} \] - 其中 \( \bar{x} \) 是平均值。 具体步骤如下： 1. 计算每个数据点与平均值的差的平方。 2. 求和。 3. 除以数据点数量。 4. 开平方根。 计算过程如下： \[ (x_1 - \bar{x})^2 = (0.26 - 0.247)^2 = 0.000121 \] \[ (x_2 - \bar{x})^2 = (0.23 - 0.247)^2 = 0.000241 \] \[ (x_3 - \bar{x})^2 = (0.28 - 0.247)^2 = 0.001089 \] \[ (x_4 - \bar{x})^2 = (0.26 - 0.247)^2 = 0.000121 \] \[ (x_5 - \bar{x})^2 = (0.21 - 0.247)^2 = 0.000241 \] \[ (x_6 - \bar{x})^2 = (0.24 - 0.247)^2 = 0.000049 \] 求和： \[ \sum (x_i - \bar{x})^2 = 0.000121 + 0.000241 + 0.001089 + 0.000121 + 0.000241 + 0.000049 = 0.001862 \] 除以数据点数量（6）： \[ \frac{0.001862}{6} = 0.0003103333 \] 开平方根： \[ s = \sqrt{0.0003103333} = 0.017616 \] 四舍五入到小数点后三位，得到 **0.002**。 ### 结论 综上所述，算术平均值为 **0.247**，标准偏差为 **0.002**。因此，正确答案是 **B: 0.247, 0.002**。 希望这个解释对你有帮助！如果有任何疑问，请随时提问。
和甲醇的氧化反应式: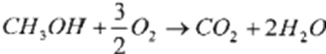
求得甲醇的 COD 法氧化率为 ( )。
A. 29.6%
B. 26.9%
C. 59.2%
D. 53.8%
A. ZnSO4 和 HCL
B. ZnSO4 和 NaOH
C. ZnSO4 和 HAC
D. SnCL2 和 NaOH
A. MTBF
B. TBFM
C. FMBT
D. MBTF。
A. 测量值一真值
B. 真值一测量值
C. 测量值一平均值
D. 平均值一真值
A. 硫酸亚铁铵
B. 硫酸亚铁
C. 邻苯二甲酸氢钾
D. 硫酸铵
A. 代表性准确性
B. 精密度准确度
C. 精密度灵敏度
D. 完整性可比性
A. 使溶液处于还原状态
B. 保证汞氧化完全
C. 防止汞的挥发
D. 还原过量的高锰酸钾
A. 有机物质总量
B. 无机物质总量
C. 有机物和无机物质总量
D. 物质总量
A. 浊度
B. 盐度
C. 黏度
D. 温度
A. 型号码
B. 动作时间
C. 动作次数
D. 大小
